Fitness-density covariance:
modifying population dynamics with spatial scale; a mechanism of
community stability; a mechanism of diversity maintenance. There is
another name for exactly the same thing: “growth-density covariance.”
Fitness-density covariance captures important aspects of variation of
population density in space. If population density is higher in
some places than others, what does that mean for the growth of the
population summed over the entire area? The theory of fitness-density
covariance shows that this variation matters if fitness of the
population varies in a space in a manner that is correlated with
variation in population density. Fitness-density covariance
measures exactly how much it matters. The concept can be used with data
from nature, and with models. The concept captures the importance of
spatial density variation in situations with any complexity. A
spatial pattern may be extremely complicated, but the bottom line is
simply how much this complicated pattern affects fitness-density
covariance.
Fitness-density covariance is, in simplest terms, the spatial
covariance between the fitness of an individual and the local
population density that it experiences. So what is fitness?
Fitness can be defined in discrete-time or continuous time. Let
us first of all examine it in discrete time. An individual at a given
location x in space, at time t, will over one unit of time
change its state. For example, it may die, or it may give birth
to a number or other offspring, or it may do all of these.
Fitness as a function of x
and t is equal to probability
that the
individual survives to time t
+ 1, plus the expected number of offspring attributed to it. Offspring
are attributed to an individual according to genomic
contributions. For asexual reproduction, genomic contributions
are unity. For sexual reproduction, selfed offspring also have unit
genomic contributions, but outcrossed offspring are counted as
half. The expectation is the statistically predicted number based
on the conditions at location x
and time t.
If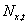 is the number of individuals at location x at time t, then the
expected number of survivors and offspring arising from them at time t + 1 is
is the number of individuals at location x at time t, then the
expected number of survivors and offspring arising from them at time t + 1 is 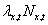 .
These individuals need not still be at location x. In general, some of them will
move. Thus,
.
These individuals need not still be at location x. In general, some of them will
move. Thus, 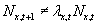 . However, if we assume for the moment that expected and actual numbers
of survivors and offspring are the same, then
. However, if we assume for the moment that expected and actual numbers
of survivors and offspring are the same, then
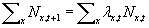
where the summation is over all spatial locations. The assumption here
is that individuals are not lost from the system. With a few
definitions, we can now simply derive our fundamental equation.
First, we define the total population as 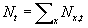 , then population density as the average number of
individuals per location:
, then population density as the average number of
individuals per location: 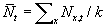 , where k is
the number of spatial locations, similarly,
, where k is
the number of spatial locations, similarly, 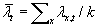 , the spatial average
fitness, and finally, the relative density as
, the spatial average
fitness, and finally, the relative density as 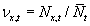 . We
can now state our
fundamental equations:
. We
can now state our
fundamental equations:
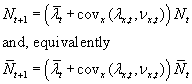 .
.
The quantity 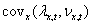 is fitness-density
covariance. We can introduce
another concept here to help understand this equation. This is the
concept of individual average fitness,
is fitness-density
covariance. We can introduce
another concept here to help understand this equation. This is the
concept of individual average fitness,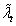 . Individual
average fitness is defined as
. Individual
average fitness is defined as  ,
i.e. simply the
number of individuals at time t
+ 1, divided by the number at the previous time. Average
individual fitness by definition relates the numbers of individuals at
different times, i.e.
,
i.e. simply the
number of individuals at time t
+ 1, divided by the number at the previous time. Average
individual fitness by definition relates the numbers of individuals at
different times, i.e.

These features mean that
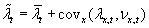 ,
,
i.e. that individual average fitness is equal to the spatial average of
fitness plus fitness-density covariance.
These equations show that averaging fitness in space is not going to
give the right answer for the rate for the growth of the
population. Growth of the population is instead given by average
individual fitness, 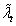 . This differs from
the average by an amount equal
to
. This differs from
the average by an amount equal
to 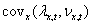 , i.e. by an amount
equal to fitness-density covariance. We
can also think of this in a little different way. We can write
, i.e. by an amount
equal to fitness-density covariance. We
can also think of this in a little different way. We can write
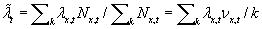 ,
,
where both expressions can be seen to be a weighted average of the
individual fitness,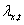 , over space, with
the weights being the local
population density. This is the way this concept was first
introduced by Chesson and Murdoch (1986).
, over space, with
the weights being the local
population density. This is the way this concept was first
introduced by Chesson and Murdoch (1986).
Continuous-time development of fitness-density covariance can be found
in Chesson et al (2005). Chesson and Murdoch (1986), Hassell et
al (1991) and Chesson et al (2005)show how fitness-density covariance
affects stability of host-parasitoid relationships. The effect of
fitness-density covariance on host-parasitoid dynamics is explained in
most detail in Chesson et al (2005). The effects of
fitness-density covariance on species coexistence are explored in
Chesson (2000), where the concept is first formally introduced, and in
Chesson et al (2005) and Snyder and Chesson (2003).
One point in the development above equated expected and actual numbers
of survivors and offspring. When is this justified? As
discussed in Chesson (1981) and Chesson (2000), this is justified in
the development above when the total population size is large.
The difference between actual and expected numbers is due to
demographic stochasticity. It can be neglected in the description
of the total population size if the total population is large.
For the calculation of fitness density covariance, the value of 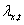 can always be the expected numbers not the actual
numbers of survivors and offspring. However, demographic
stochasicity cannot be neglected in the calculation of the local
population sizes,
can always be the expected numbers not the actual
numbers of survivors and offspring. However, demographic
stochasicity cannot be neglected in the calculation of the local
population sizes,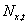 . Demographic
stochasiticity will affect this value, and normally
. Demographic
stochasiticity will affect this value, and normally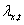 will
be a function of it. In this way, demographic stochasiticity will
affect fitness-density covariance through its effects on local
population densities. Ignoring demographic stochasicity in the
calculation of local population densities is thus only justified if
local population densities are large, or
will
be a function of it. In this way, demographic stochasiticity will
affect fitness-density covariance through its effects on local
population densities. Ignoring demographic stochasicity in the
calculation of local population densities is thus only justified if
local population densities are large, or 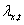 does
not depend on local population density.
does
not depend on local population density.
References
Chesson,
P.L.1981. Models for spatially distributed populations: the effect of
within-patch variability. Theor. Pop. Biol. 19, 288-325.
Chesson,
P.L., Murdoch, W.W. 1986. Aggregation of risk: relationships
among host-parasitoid models. American Naturalist 127, 696 - 715.
Chesson,
P. 2000.
General theory of competitive coexistence in spatially varying
environments.
Theoretical Population Biology 58, 211-237
Chesson, P., Donahue,
M., Melbourne, B., Sears, A. 2005. Scale
transition theory for understanding mechanisms in
metacommunities. In Holyoak, M, Leibold, M.A., Holt, R.D., eds,
Metacommunities: spatial dynamics and ecological communities, pp
279-306.
Hassell,
M.P., May,
R.M., Pacala, S.W., Chesson, P.L. 1991. The
persistence of host-parasitoid associations in patchy environments. I.
A general criterion. American Naturalist 138, 568-583.
Snyder,
R.E. and
Chesson, P. 2003. Local dispersal can facilitate coexistence in the
presence of
permanent spatial heterogeneity. Ecology Letters 6,301–309.
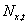 is the number of individuals at location x at time t, then the
expected number of survivors and offspring arising from them at time t + 1 is
is the number of individuals at location x at time t, then the
expected number of survivors and offspring arising from them at time t + 1 is 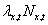 .
These individuals need not still be at location x. In general, some of them will
move. Thus,
.
These individuals need not still be at location x. In general, some of them will
move. Thus, 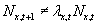 . However, if we assume for the moment that expected and actual numbers
of survivors and offspring are the same, then
. However, if we assume for the moment that expected and actual numbers
of survivors and offspring are the same, then 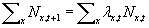
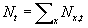 , then population density as the average number of
individuals per location:
, then population density as the average number of
individuals per location: 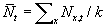 , where k is
the number of spatial locations, similarly,
, where k is
the number of spatial locations, similarly, 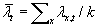 , the spatial average
fitness, and finally, the relative density as
, the spatial average
fitness, and finally, the relative density as 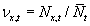 . We
can now state our
fundamental equations:
. We
can now state our
fundamental equations: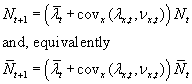 .
.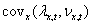 is fitness-density
covariance. We can introduce
another concept here to help understand this equation. This is the
concept of individual average fitness,
is fitness-density
covariance. We can introduce
another concept here to help understand this equation. This is the
concept of individual average fitness,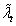 . Individual
average fitness is defined as
. Individual
average fitness is defined as  ,
i.e. simply the
number of individuals at time t
+ 1, divided by the number at the previous time. Average
individual fitness by definition relates the numbers of individuals at
different times, i.e.
,
i.e. simply the
number of individuals at time t
+ 1, divided by the number at the previous time. Average
individual fitness by definition relates the numbers of individuals at
different times, i.e.
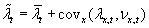 ,
,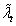 . This differs from
the average by an amount equal
to
. This differs from
the average by an amount equal
to 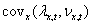 , i.e. by an amount
equal to fitness-density covariance. We
can also think of this in a little different way. We can write
, i.e. by an amount
equal to fitness-density covariance. We
can also think of this in a little different way. We can write 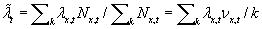 ,
, 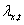 , over space, with
the weights being the local
population density. This is the way this concept was first
introduced by Chesson and Murdoch (1986).
, over space, with
the weights being the local
population density. This is the way this concept was first
introduced by Chesson and Murdoch (1986). 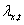 can always be the expected numbers not the actual
numbers of survivors and offspring. However, demographic
stochasicity cannot be neglected in the calculation of the local
population sizes,
can always be the expected numbers not the actual
numbers of survivors and offspring. However, demographic
stochasicity cannot be neglected in the calculation of the local
population sizes,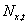 . Demographic
stochasiticity will affect this value, and normally
. Demographic
stochasiticity will affect this value, and normally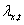 will
be a function of it. In this way, demographic stochasiticity will
affect fitness-density covariance through its effects on local
population densities. Ignoring demographic stochasicity in the
calculation of local population densities is thus only justified if
local population densities are large, or
will
be a function of it. In this way, demographic stochasiticity will
affect fitness-density covariance through its effects on local
population densities. Ignoring demographic stochasicity in the
calculation of local population densities is thus only justified if
local population densities are large, or 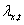 does
not depend on local population density.
does
not depend on local population density.